Par exemple, dans le calcul de ∫ x 2 cos (2 x) d x , une erreur serait de penser que puisque 2 x est la dérivée de x 2 , on peut faire un changement de variable. Ici, pour que le changement de variable fonctionne, il faudrait que x 2 soit la dérivée de 2 x . Ce n'est pas le cas donc la méthode du changement de.. CHAPITRE VI. THÉORÈME DU CHANGEMENT DE VARIABLE 2 de Lebesgue. Cette propriété n'est pas vraie pour tout homéomor-phisme, et c'est pourquoi nous supposerons ici que φ est un difféo- morphisme de classe C1 (cette hypothèse est un peu forte ; il suffi- rait de supposer que φ est un homéomorphisme de classe C1). 1.2.
Intégration par Changement de variable

Théorème de changement de variables somme et différence de deux variables exponentielles YouTube

Intégration par changement de variable Cas complexes YouTube

Intégration par changement de variable 7 YouTube

Intégration par changement de variable 2 YouTube

Changement de variable dans une équation différentielle partie 3 YouTube

Équations différentielles et changement de variable partie 1 YouTube

Règles de Bioche changement de variable t = tan(x/2) pour calculer une intégrale YouTube

Démonstration du théorème du changement de variables. YouTube

Changement de variable. Intégration d'une fonction rationnelle trigonométrique en ( sin x , cos

Bien DÉTECTER un CHANGEMENT DE VARIABLE pour RÉSOUDRE des INTÉGRALES Méthode + Exemple Maths
![[MathSVT] Fic 9. Changement de variables YouTube [MathSVT] Fic 9. Changement de variables YouTube](https://i.ytimg.com/vi/n09CCoqDyFU/maxresdefault.jpg)
[MathSVT] Fic 9. Changement de variables YouTube

Exercice Calcul d'une primitive changement de variables YouTube

Exercice Calcul intégral et changements de variables YouTube
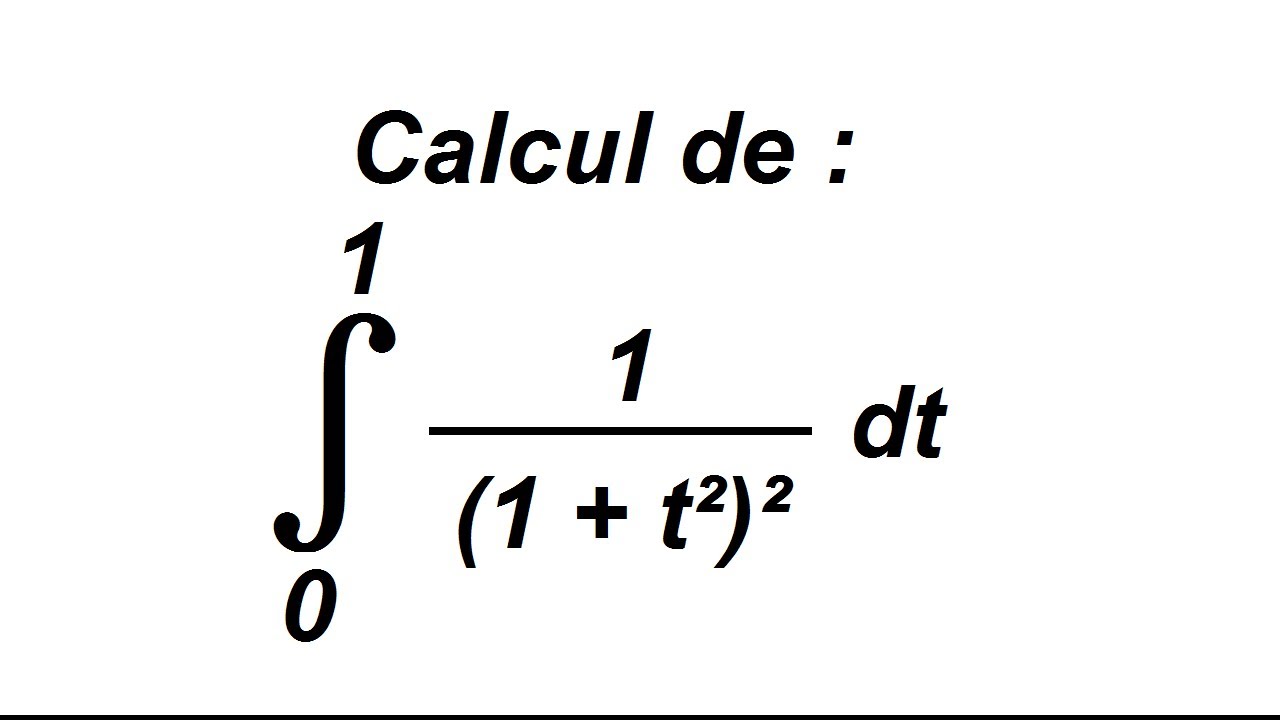
Intégrale de 1/(1+t²)² avec changement de variable YouTube

Exercice Intégration par Changement de Variable YouTube

Exercice d’application du théorème de changement de variables sur une intégrale double YouTube

Équations différentielles. Exercice corrigé 2. Changement de variable. YouTube

Intégration par changement de variable Cours et Exercices Corrigés 2 Bac SM [Partie4

Le CHANGEMENT DE VARIABLE pour RÉSOUDRE des INTÉGRALES Méthode + Exemple Maths Prépa Licence
En mathématiques, et plus précisément en analyse, l' intégration par changement de variable est un procédé d' intégration qui consiste à considérer une nouvelle variable d'intégration, pour remplacer une fonction de la variable d'intégration initiale. Ce procédé est un des outils principaux pour le calcul explicite d'intégrales.. En appliquant la règle de Bioche on effectue le changement de variable suivant afin de convertir la fonction à intégrer en une fraction rationnelle en t : Rappel de trigonométrie : pour tout x réel on a sin (2.arctan (x)) = (2.x)/ (1+x²) L'intégrale I devient alors une simple fraction rationnelle en t :